L'ottava meraviglia del mondo
L'ottava meraviglia del mondo
La magia dell'interesse composto
Preferiresti ricevere 10.000 euro al giorno per un mese oppure 1 centesimo di euro che raddoppia ogni giorno per un mese?
La risposta può sembrare scontata, ma dimostra l’enorme differenza che possono avere una crescita lineare ed una esponenziale.
Ma andiamo con ordine.
La magia dell’interesse composto
Probabilmente hai già famigliarità con il concetto di interesse.
È il principio su cui si basano tanto mutui e prestiti quanto gli investimenti finanziari: ottenere un rendimento da una somma di denaro.
Se ci pensi, un prestito e un’obbligazione sono esattamente la stessa cosa, ma vista da due prospettive diverse: una parte presta un capitale all’altra e in cambio le chiede un interesse e l’impegno a restituirle il capitale dopo un certo lasso di tempo.
Nel caso del prestito sei tu a chiedere un capitale e a pagare un interesse, nel caso dell’obbligazione tu presti il capitale e ottieni un rendimento.
Interesse semplice e interesse composto
Quello che ottieni da un’obbligazione è un interesse semplice perché l’interesse (cedola) è calcolato sempre sul capitale iniziale.
Se sottoscrivi un’obbligazione ad un tasso fisso del 2% e una scadenza di 5 anni per 10.000 euro, ogni anno riceverai una cedola del 2%, pari a 200 euro (lorde) e alla scadenza riceverai il rimborso di 10.000 euro.
Alla fine dei 5 anni avrai 10.000 euro + 1.000 euro di interessi (200 x 5).
L’interesse composto funziona in modo leggermente diverso: l’interesse è calcolato sul capitale iniziale più gli interessi già maturati.
Si tratta di una differenza apparentemente minuscola, ma dai risvolti eccezionali.
Se investi gli stessi 10.000 euro in un conto deposito con un interesse annuo del 2%, dopo 5 anni non ti troverai con 11.000 euro, ma con 11.040 euro.
La differenza è minima, solo 40 euro, ed è dovuta al fatto che in questi 5 anni hai ottenuto un rendimento, oltre che sul capitale iniziale, anche sugli interessi maturati di anno in anno.
Il primo anno ottieni 200 euro, il secondo 204, poi 208, 212 e infine 216.
Totale 1.040 euro.
Quei 40 euro possono non sembrare molti, ma l’interesse composto funziona come una palla di neve su un pendio innevato: mano a mano che scende acquista velocità e dimensioni.
Dal punto di vista matematico, la capitalizzazione semplice è una funzione lineare, mentre la capitalizzazione composta è una funzione esponenziale.
Torniamo ora alla domanda iniziale:
Preferiresti ricevere 10.000 euro al giorno per un mese oppure 1 centesimo di euro che raddoppia ogni giorno per un mese?
Se scegliessi la risposta più scontata, la prima, alla fine del mese ti troveresti con 310.000 euro. Non male.
Se invece conoscessi la magia dell’interesse composto, sicuramente sceglieresti di partire con un centesimo e di raddoppiarlo ogni giorno per 1 mese.
In questo modo, alla fine del mese ti troveresti con la bellezza di oltre 10 milioni:
10.737.418 euro per l’esattezza,
35 volte quello che avresti ottenuto ricevendo 10.000 euro al giorno.
Il motivo per cui l’esempio del centesimo ha un risultato così strabiliante è che utilizza un rendimento eccezionale, pari al 100% al giorno.
I numeri del mondo reale sono decisamente più contenuti.
Cosa rende “magico” l’interesse composto
Sfruttare l’interesse composto accelera sempre la crescita del tuo denaro rispetto all’interesse semplice, ma ci sono tre fattori che lo rendono “magico”:
· Un tasso d’interesse levato
· Un capitale iniziale maggiore o l’aggiunta di capitale negli anni
· Il TEMPO
Se l’orizzonte di tempo è breve e il rendimento ottenuto modesto, la differenza tra interesse semplice e composto non è sostanziale.
Supponi di far crescere i tuoi risparmi per 10 anni nelle seguenti condizioni:
Interesse composto e capitalizzazione annuale degli interessi
Ovviamente partire con un capitale maggiore è di grade aiuto. Ma anche ottenere un rendimento del 6% anziché del 2% fa un’enorme differenza.
Supponi ora di lasciar lavorare i tuoi risparmi per 30 anni. E che tu sia in grado di aggiungere al capitale iniziale 5.000 euro ogni anno:
Interesse composto e capitalizzazione annuale degli interessi
Anche nel mondo reale, con un lungo orizzonte di tempo, un rendimento adeguato e la possibilità di contribuire periodicamente, è possibile ottenere risultati eccezionali.
In 30 anni, 100.000 euro iniziali più 5.000 euro all’anno, con un rendimento del 6% possono trasformarsi in 1 milione di euro.
Lo stesso risultato può essere ottenuto con un capitale iniziale molto più modesto:
Interesse composto e capitalizzazione annuale degli interessi
20.000 euro iniziali più 5.000 euro all’anno, con un rendimento del 6%, in 40 anni diventano 1 milione di euro (979.524 €).
Aggiungendo 10 anni e investendo nel complesso 30.000 euro in meno ottieni lo stesso importo finale.
Differenza tra interesse semplice e interesse composto
La scelta di reinvestire gli interessi maturati (interesse composto) o di non farlo (interesse semplice) ha un effetto significativo sul risultato finale:
Capitalizzazione annuale degli interessi
La differenza nel risultato finale tra interesse semplice e composto cresce all’aumentare del tempo d’investimento e del rendimento ottenuto.
È molto ridotta nel caso di un rendimento del 2%, ma molto significativa con un rendimento del 6% e aumenta al crescere dell’orizzonte temporale.
Un’altra variabile da considerare nel calcolo dell’interesse composto è la periodicità con cui vengono capitalizzati gli interessi.
Mi spiego meglio: se gli interessi vengono capitalizzati annualmente (come negli esempi fatti fino ad ora), gli interessi maturati inizieranno a rivalutarsi solo passato un anno.
Se invece la capitalizzazione avviene mensilmente, gli interessi maturati nel primo mese verranno messi immediatamente al lavoro e inizieranno a produrre a loro volta altri interessi.
Osserva la differenza che si genera nel tempo tra capitalizzare gli interessi annualmente o mensilmente:
Anche in questo caso, più lungo è l’orizzonte temporale e maggiore è la differenza.
Prima si mette al lavoro il capitale e più tempo lo si lascia lavorare e maggiore sarà il risultato finale.
Per lo stesso principio, effettuare un versamento all’anno di 5.000€ apporta un beneficio minore rispetto al fare un versamento mensile per un importo totale di 5.000€ all’anno.
QUI puoi fare tutte le simulazioni che desideri.
In conclusione
Albert Einstein ha definito l’interesse composto l’ottava meraviglia del mondo per il modo straordinario in cui può trasformare piccole somme in enormi ricchezze.
Nel mondo reale hai tre modi per aumentare il risultato finale del tuo investimento:
- risparmiando di più,
- cercando rendimenti maggiori e sostenibili nel tempo
- lasciando che i tuoi risparmi crescano più a lungo
"La mia ricchezza deriva da una combinazione di 3 fattori:
vivere in America, alcuni geni fortunati e l’interesse composto."Warren Buffett
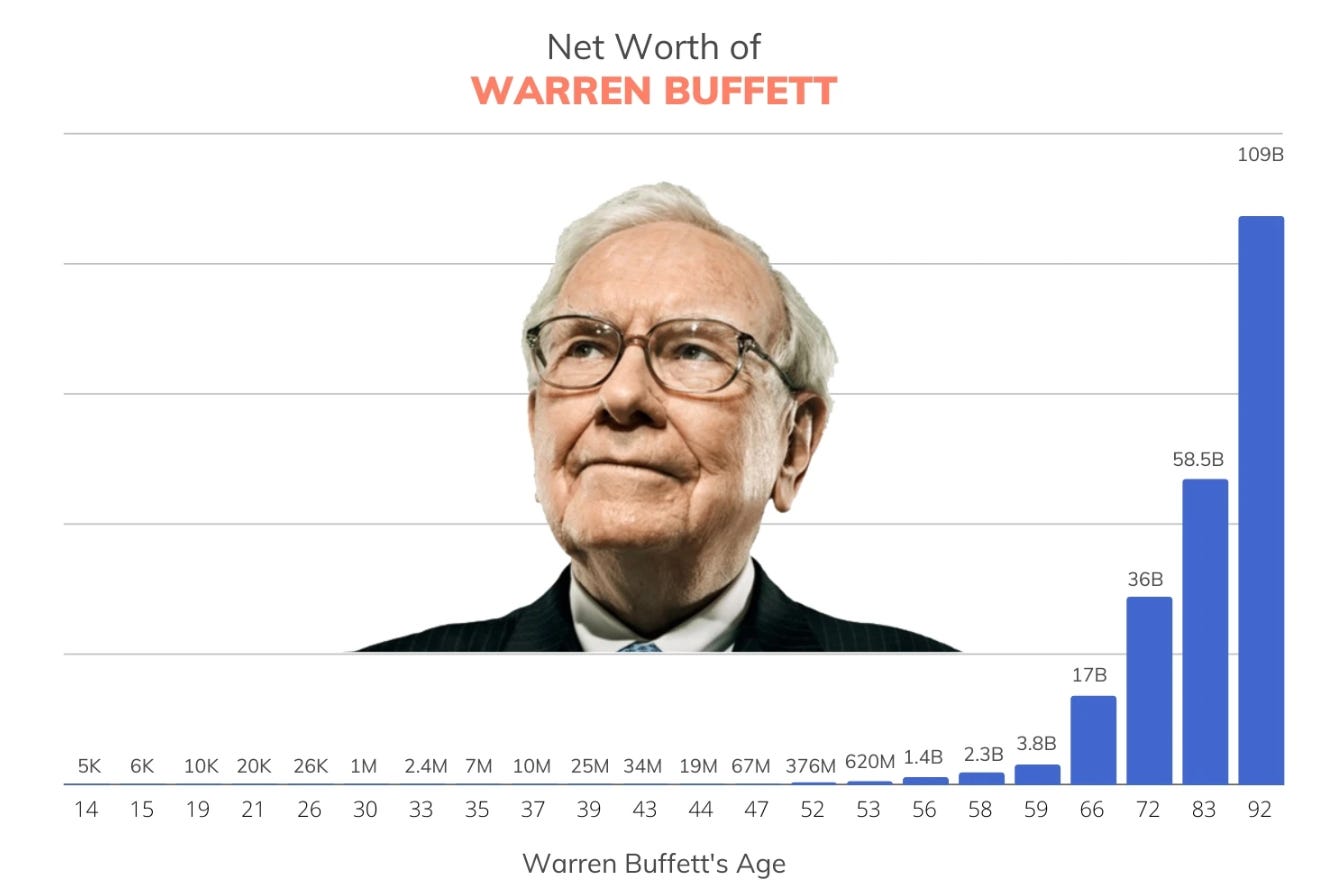
Warren Buffett negli anni ha ottenuto rendimenti eccezionali con i suoi investimenti, ma il suo vero superpotere è stato il tempo per cui ha potuto far lavorare l’interesse composto a suo favore:
ha infatti accumulato il 99% della sua ricchezza totale dopo i 50 anni
La ricchezza di Warren Buffett nel tempo
https://finmasters.com/warren-buffett-net-worth/#gref
Curiosità: la “regola del 72”
Quanto tempo ci vorrà per raddoppiare i tuoi soldi?
Dividendo il numero 72 per il rendimento medio annuo si ottiene una stima approssimativa.
Se ottieni un rendimento del 2%, ci vorranno 36 anni per raddoppiare il tuo capitale (72/2 = 36)
Se invece ottieni un rendimento del 6% ci vorranno 12 anni (72/6 = 12)
La stessa regola può essere usata per farti un’idea di quanto sia dannosa l’inflazione per i tuoi risparmi:
con un’inflazione media del 2% i tuoi risparmi improduttivi perdono metà del loro potere d’acquisto in 36 anni (73/2 = 36)
con un’inflazione media del 4% i tuoi risparmi improduttivi perdono metà del loro potere d’acquisto in 18 anni (73/4 = 18)
Grazie per aver letto “Investire con Intelligenza”
Se hai trovato interessante questo articolo, con le icone in cima e in fondo alla pagina, puoi lasciare un like ❤️, un commento 💬
oppure condividerlo 📣
❤️ 𝐈𝐧𝐯𝐞𝐬𝐭𝐢𝐫𝐞 𝐜𝐨𝐧 𝐈𝐧𝐭𝐞𝐥𝐥𝐢𝐠𝐞𝐧𝐳𝐚 🧠:
𝙥𝙞𝙡𝙡𝙤𝙡𝙚 𝙨𝙚𝙩𝙩𝙞𝙢𝙖𝙣𝙖𝙡𝙞 𝙙𝙞 𝙗𝙪𝙤𝙣 𝙨𝙚𝙣𝙨𝙤 𝙛𝙞𝙣𝙖𝙣𝙯𝙞𝙖𝙧𝙞𝙤 📧